Introduction

In 2022, ByteDance proposed an issue recommending that Golang adopt SwissTable for its map implementation. In 2023, Dolt published a blog post titled SwissMap: A Smaller, Faster Golang Hash Table, detailing their design of a swisstable, which garnered widespread attention. The Go core team is reevaluating the swisstable design and has added some related code in the runtime. With some free time during the holidays, let’s delve deeper into the principles, compare it to the runtime map, and understand why it might become the standard for map implementation.

This article was first published in the Medium MPP plan. If you are a Medium user, please follow me on Medium. Thank you very much.

This article will not fully explain the principles of hashtable or swisstable. A basic understanding of hashtable is required.

A hashtable provides a mapping from a key to a corresponding value by converting the key to some “position” using a hash function. From this position, we can directly retrieve the desired value.

Traditional Hashtable

A hashtable provides a mapping from a key to a corresponding value by converting the key to some “position” using a hash function. However, even if the hash function is perfect, conflicts are still inevitable when mapping an infinite number of keys into a finite memory space: two different keys will be mapped to the same position. To solve this, traditional hashtables have several conflict resolution strategies, most commonly chaining and linear probing.

Chaining

Chaining is the most common method where if multiple keys map to the same position, these keys and values are stored in a linked list. During lookups, the hash function is used to find the position, and then the linked list at that position is traversed to find the matching key. Its structure is similar to this:

Figure 1: Chaining implementation of hashtable

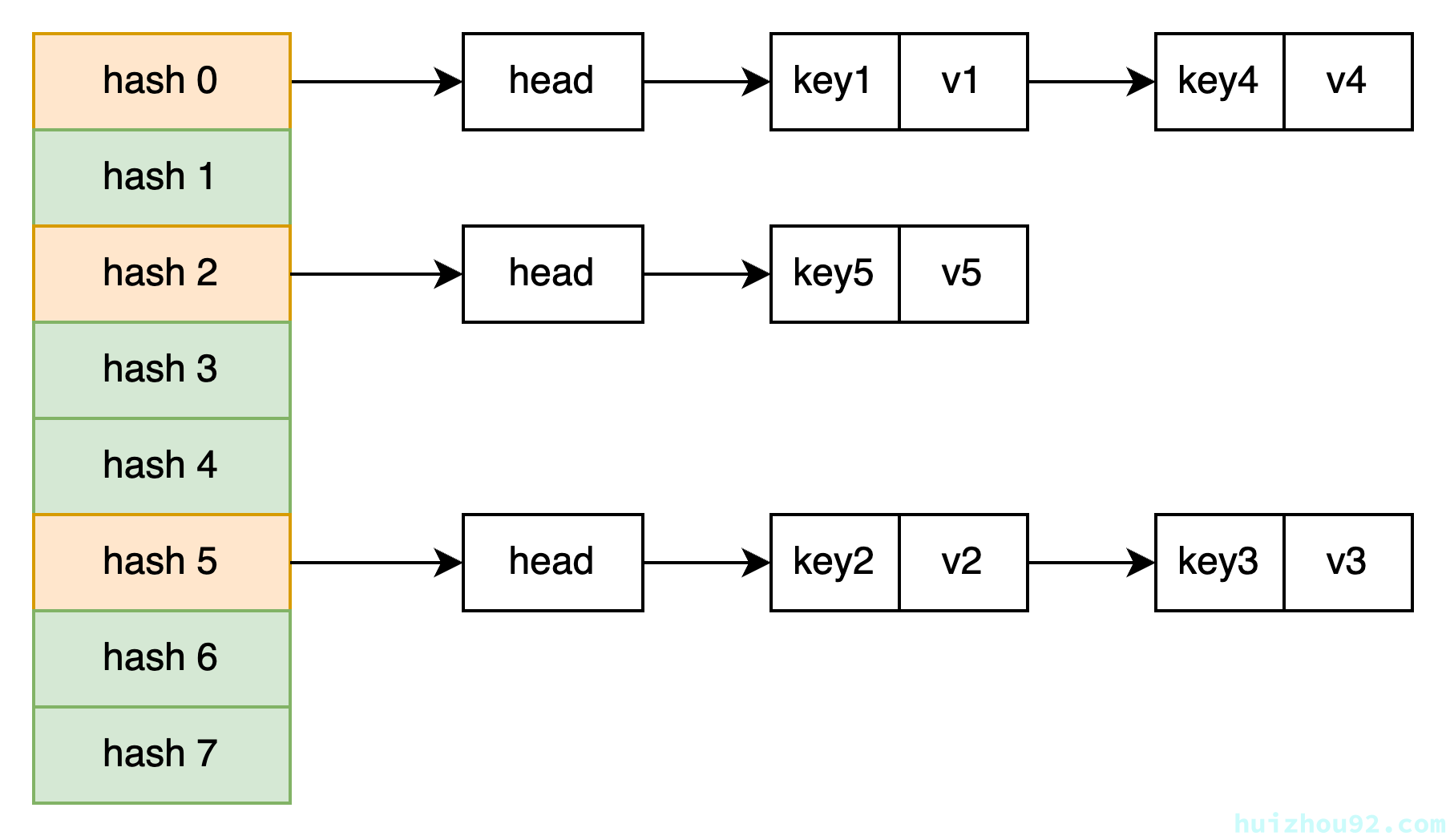
Chaining is straightforward to implement, with fewer boundary conditions to consider. Data insertion and deletion are quick, using head insertion to add new entries and adjusting the next pointer for deletion. Chaining can also prevent performance degradation by converting overly long chains into search trees. However, chaining is not cache-friendly, and performance can be affected if there are many conflicts. Different slots can be widely spread in memory, leading to poor spatial locality of the data structure overall.

Linear Probing

Linear probing is another standard hash table conflict resolution method. Unlike chaining, when a hash conflict occurs, it searches sequentially from the conflict position until it finds an empty slot or loops back to the conflict position. At this point, it resizes and rehashes the entries.

Figure 2: Linear probing animation

Lookups work similarly: calculate the hash position for the key and then compare each key starting from that position, skipping any deleted entries until an empty slot is reached, indicating the key is not in the table. Deletion uses a tombstone marker.

Figure 3: Linear probing lookup animation

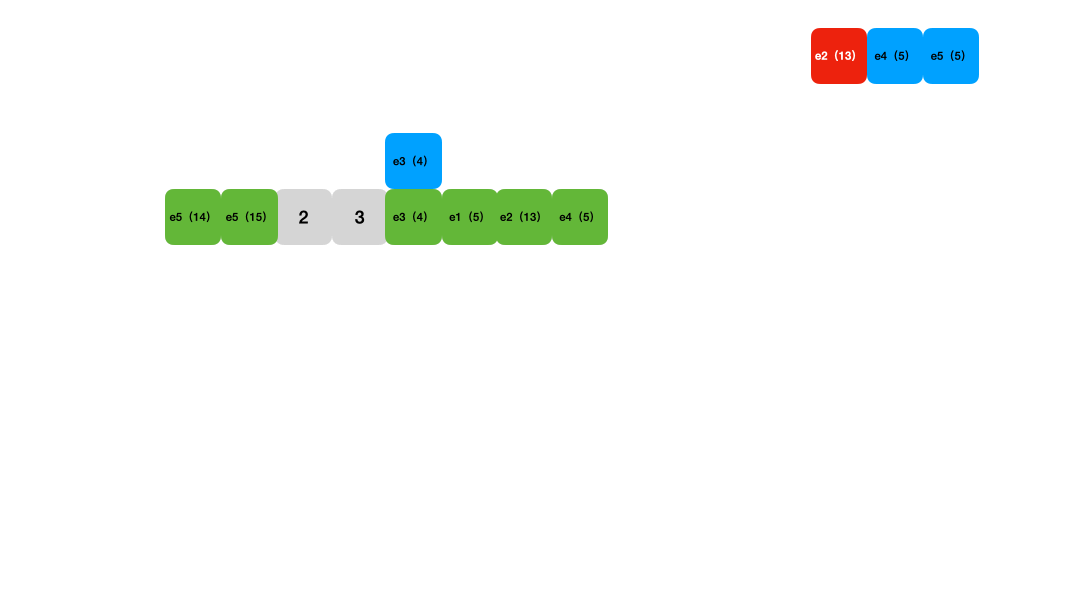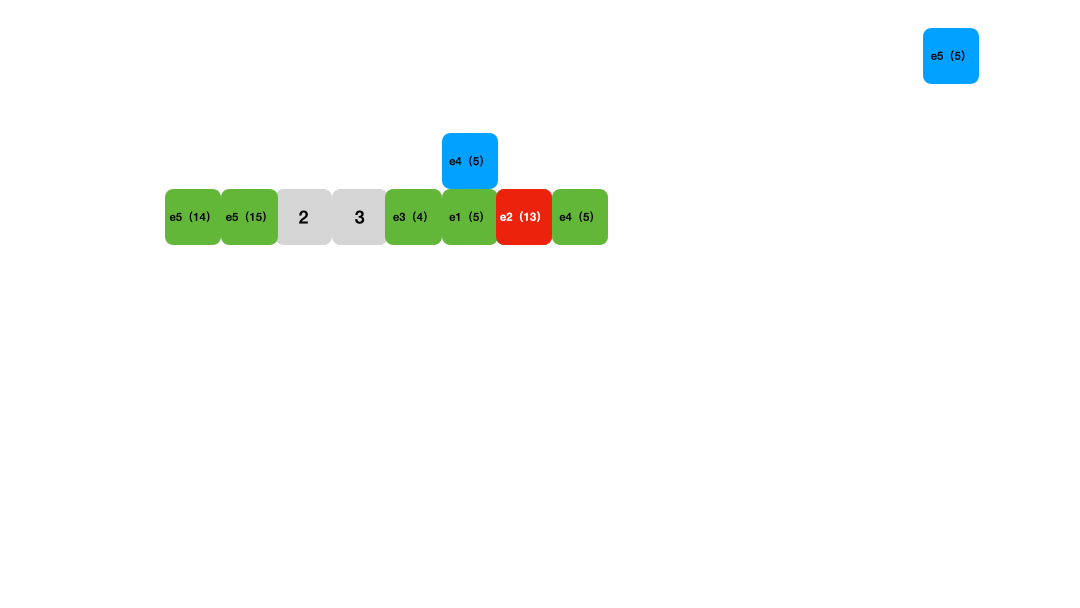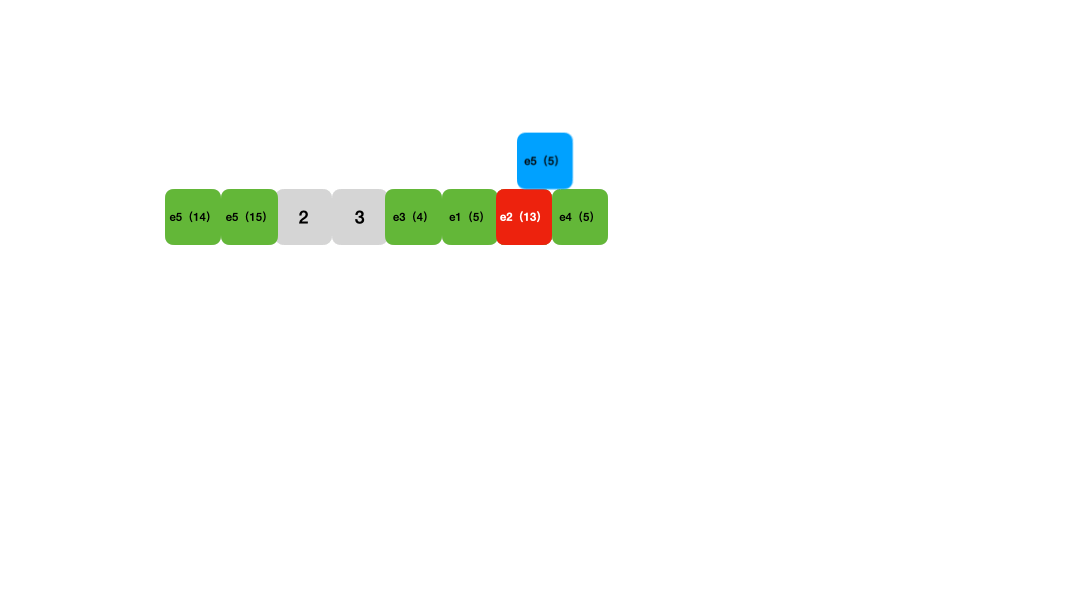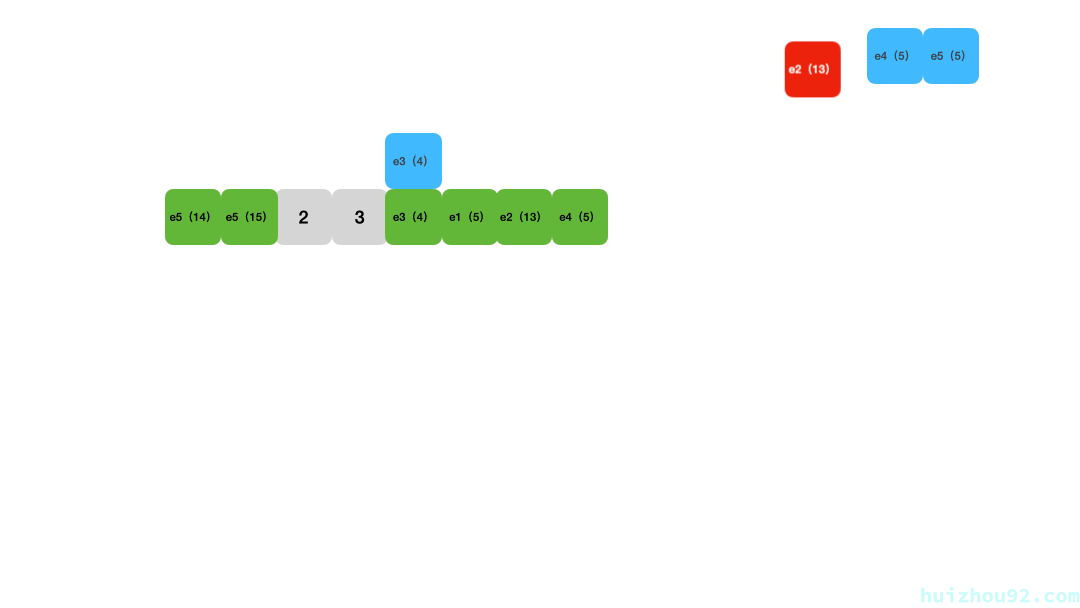
Linear probing has comparable time complexity to chaining. Its advantages include being cache-friendly and implementable with tight data structures like arrays. However, its drawbacks are:

1. Complex implementation with three states for a slot: occupied, empty, and deleted.
2. Chain reaction of conflicts, leading to more frequent resizing than chaining and potentially more significant memory usage.
3. Higher likelihood of lookup process degradation to O(n) without the ability to convert heavily conflicted areas into search trees.

Many libraries use chaining due to the difficulties with element deletion and conflict chain reactions in linear probing. Despite its drawbacks, linear probing’s cache friendliness and memory efficiency provide significant performance advantages on modern computers, leading to its use in languages like golang and Python.

Go Map Data Storage

Let’s recap how Go Map stores data:

**Figure 4: Go map **

Quick summary:

• Go map uses a hash function to map keys to multiple buckets, each with a fixed number of key-value slots for storage.
• Each bucket stores up to 8 key-value pairs. The conflicting keys and values are stored within the same bucket when conflicts occur.
• The map uses a hash function to compute the key’s hash value and locate the corresponding bucket.
• If a bucket is complete (all 8 slots used), an overflow bucket is generated to continue storing new key-value pairs.
• For lookups, the key’s hash value is calculated, the corresponding bucket is determined, and each slot within the bucket is checked. If there is an overflow bucket, its keys are also checked sequentially.

SwissTable: An Efficient Hashtable Implementation

SwissTable is a hashtable implementation based on an improved linear probing method. Its core idea is to optimize performance and memory usage by enhancing the hashtable structure and metadata storsage. SwissTable uses a new metadata control mechanism to significantly reduce unnecessary key comparisons and leverages SIMD instructions to boost throughput.

Reviewing the two standard hashtable implementations shows they either waste memory, need to be cache-friendly or suffer performance drops in lookup, insertion, and deletion operations after conflicts. These issues persist even with a “perfect hash function.” Using a suboptimal hash function dramatically increases the probability of key conflicts and worsens performance, possibly even falling short of linear searches in an array.

The industry sought a hash table algorithm that was friendly to cache and resistant to lookup performance degradation. Many focused on developing better hash functions close to “perfect hash function” quality while optimizing calculation performance; others worked on improving the hash table’s structure to balance cache friendliness, performance, and memory usage. swisstable belongs to the latter.

SwissTable’s time complexity is similar to linear probing, while its space complexity is between chaining and linear probing. The implementation I’ve referenced is primarily based on dolthub/swiss.

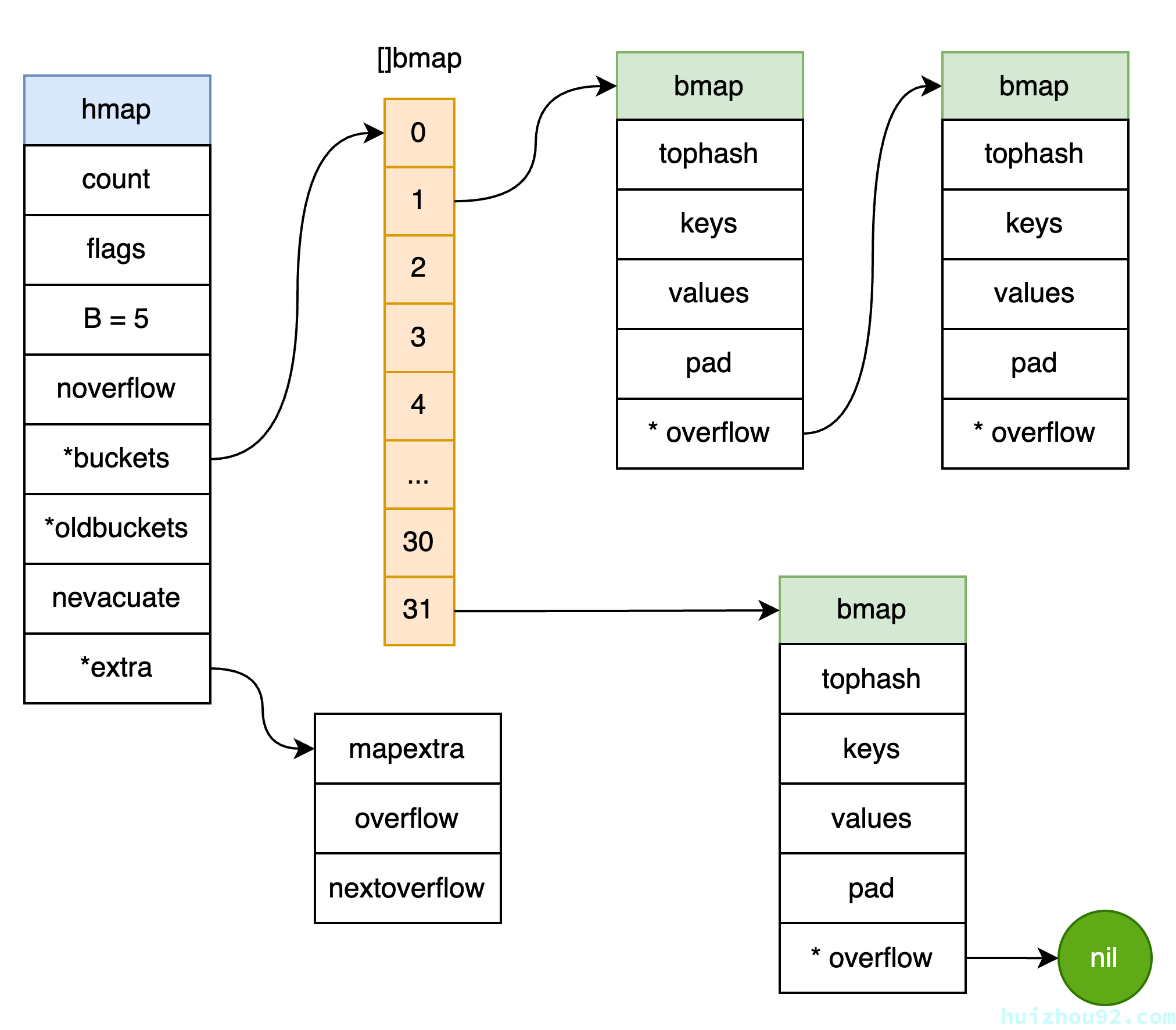
Basic Structure of SwissTable

Although the name has changed, swisstable is still a hashtable utilizing an improved linear probing method for hash collisions. Its underlying structure resembles an array. Now, let’s delve into the structure of swisstable:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15

type Map[K comparable, V any] struct {  
    ctrl     []metadata  
    groups   []group[K, V]  
    hash     maphash.Hasher[K]  
    resident uint32   
    dead     uint32   
    limit    uint32   
} 

type metadata [groupSize]int8  

type group[K comparable, V any] struct {  
    keys   [groupSize]K  
    values [groupSize]V  
}

In swisstable, ctrl is an array of metadata, corresponding to the group[K, V] array. Each group has 8 slots.

The hash is divided into 57 bits for H1 to determine the starting groups, and the remaining 7 bits called H2, stored in metadata as the hash signature of the current key for subsequent search and filtering.

The key advantage of swisstable over traditional hash tables lies in the metadata called ctrl. Control information includes:

• Whether a slot is empty: 0b10000000
• Whether a slot has been deleted: 0b11111110
• The key’s hash signature (H2) in a slot: 0bh2

The unique values of these states allow the use of SIMD instructions, maximizing performance.

Adding Data

The process of adding data in swisstable involves several steps:

1. Calculate the hash value and split it into h1 and h2. Using h1, determine the starting groups.
2. Use metaMatchH2 to check the current group’s metadata for a matching h2. If found, further check for the matching key and update the value if they match.
3. If no matching key is found, use metaMatchEmpty to check for empty slots in the current group. Insert the new key-value pair if an empty slot is found and update the metadata and resident count.
4. If no empty slots are available in the current group, perform linear probing to check the next groups.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40

func (m *Map[K, V]) Put(key K, value V) {  
    if m.resident >= m.limit {  
        m.rehash(m.nextSize())  
    }  
    hi, lo := splitHash(m.hash.Hash(key))  
    g := probeStart(hi, len(m.groups))  
    for { // inlined find loop  
        matches := metaMatchH2(&m.ctrl[g], lo)  
        for matches != 0 {  
            s := nextMatch(&matches)  
            if key == m.groups[g].keys[s] { // update  
                m.groups[g].keys[s] = key  
                m.groups[g].values[s] = value  
                return  
            }  
        }  
        matches = metaMatchEmpty(&m.ctrl[g])  
        if matches != 0 { // insert  
            s := nextMatch(&matches)  
            m.groups[g].keys[s] = key  
            m.groups[g].values[s] = value  
            m.ctrl[g][s] = int8(lo)  
            m.resident++  
            return  
        }  
        g += 1 // linear probing  
        if g >= uint32(len(m.groups)) {  
            g = 0  
        }  
    }  
}
func metaMatchH2(m *metadata, h h2) bitset {  
    return hasZeroByte(castUint64(m) ^ (loBits * uint64(h)))  
}

func nextMatch(b *bitset) uint32 {  
    s := uint32(bits.TrailingZeros64(uint64(*b)))  
    *b &= ^(1 << s)  
    return s >> 3   
}

Although the steps are few, they involve complex bit operations. Normally, h2 needs to be compared with all keys sequentially until the target is found. swisstable cleverly achieves this by:

• Multiplying h2 by 0x0101010101010101 to get a uint64, allowing simultaneous comparison with 8 ctrl values.
• Performing xor with meta. If h2 exists in metadata, the corresponding bit will be zero. The metaMatchH2 function helps us understand this process.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22

func TestMetaMatchH2(t *testing.T) {
    metaData := make([]metadata, 2)
    metaData[0] = [8]int8{0x7f, 0, 0, 0x7f, 0, 0, 0, 0x7f}
    m := &metaData[0]
    h := 0x7f
    metaUint64 := castUint64(m)
    h2Pattern := loBits * uint64(h)
    xorResult := metaUint64 ^ h2Pattern
    fmt.Printf("metaUint64: %b\n", xorResult)
    r := hasZeroByte(xorResult)
    fmt.Printf("r: %b\n", r)
    for r != 0 {  
        fmt.Println(nextMatch(&r))  
    }
}
----
output
// metaUint64: 00000000 11111110 11111110 11111110 0000000 01111111 01111111 00000000
// r: 10000000 00000000 00000000 00000000 10000000 00000000 00000000 10000000
// 0
// 3
// 7

Advantages of SwissTable

Reviewing SwissTable implementation reveals several key benefits:

• Operations are shifted from slots to ctrl, which are smaller and easily placed in the CPU cache, speeding up operations despite the additional step of locating slots.
• Records hash signatures, reducing meaningless key comparisons—the main cause of linear probing performance drops.
• Batch operations on ctrl for slots increase throughput significantly.
• Metadata and memory layout are optimized for SIMD instructions, maximizing performance.
• Slot optimizations, such as compressing large data, increase cache hit rates.

swisstable solves spatial locality issues and exploits modern CPU features for batch element operations, significantly boosting performance.

Finally, running a benchmark on a local MacBook M1 (without SIMD support) shows significant performance improvements in large map scenarios.

Figure 5: Official swisstable benchmark

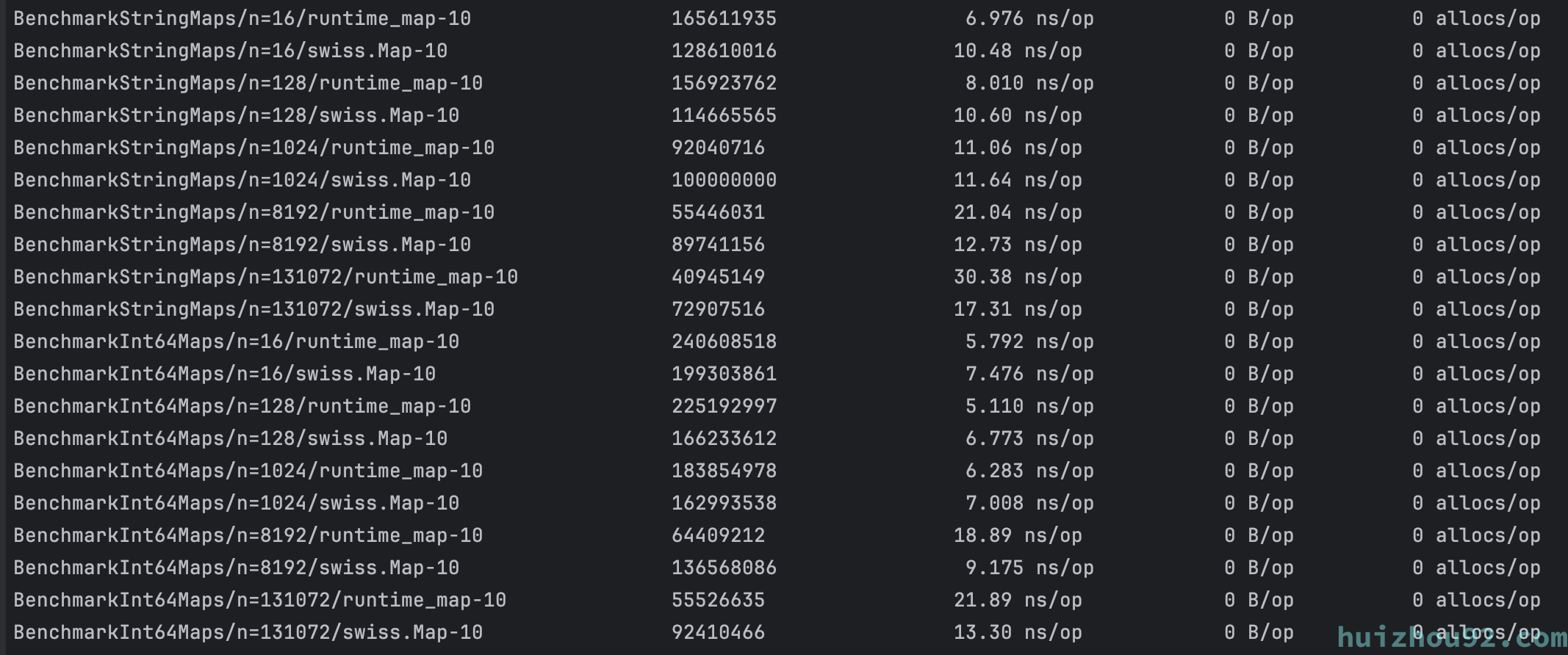
Conclusion

Currently, the official implementation of swisstable in Go is still under discussion, and there are a few community implementations like concurrent-swiss-map and swiss. However, they are not perfect; in small map scenarios, swisstable may even underperform compared to runtime_map. Nonetheless, the potential demonstrated by swisstable in other languages indicates that it is worth anticipation.

References

• Dolthub: SwissMap
• SwissTable principles: Abseil SwissTables
• Original SwissTable proposal at cppcon: cppcon talk
• Improvements to SwissTable algorithm: YouTube link
• Bit manipulation primer: Stanford Bit Hacks
• Hash function comparisons: Hash function tests
• An additional bit manipulation article: Fast Modulo Reduction