Background

Imagine a scenario with 1 million Uber drivers, where the driver client reports data every 10 minutes. If a driver does not report data within 10 minutes, the server sets that driver to an offline status and does not dispatch rides to them.
How can we implement this functionality?

Usually, we would use third-party components such as redis zset to accomplish this, but what if we don’t use third-party components? What about just using memory? There are probably several options:

Using a Timer

1. Utilize a Map<uid, last_time> to track the last report time for each UID.
2. Update this Map in real-time whenever a user with UID reports data.
3. Start a timer that periodically scans this Map to check if each UID’s last report time exceeds 30 seconds. If it does, execute a timeout handling process.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17

var (
    userMap sync.Map
    timeout = 10 * time.Minute
)

func checkTimeout() {
    now := time.Now().Unix()
    userMap.Range(func(key, value any) bool {
        uid := key.(string)
        lastTime := value.(int64)
        if now-lastTime > int64(timeout) {
            fmt.Printf("User %s timed out. Last reported at %d\n", uid, lastTime)
            userMap.Delete(uid) 
        }
        return true
    })
}

Drawback: This method is inefficient since it requires periodically scanning the entire map, resulting in high time complexity.

Using Goroutine Management

Another approach is to allocate a Goroutine for each driver to manage their heartbeat timeout.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14

timer := time.NewTimer(timeout * time.Second)
for {
    select {
    case <-heartbeat: // Received heartbeat signal
        if !timer.Stop() {
            <-timer.C
        }
        timer.Reset(timeout * time.Second)
    case <-timer.C: // Timeout
        fmt.Printf("Driver %s timed out.\n", uid)
        break
    }
}
userMap.Delete(uid)

Drawback: Although this eliminates polling, creating a Goroutine for each driver consumes significant memory when the number of drivers is very high. Additionally, creating and deleting timers operates at O(log n) time complexity, impacting efficiency.

After this groundwork, we finally arrive at our main subject: the Time Wheel.

Time Wheel Algorithm

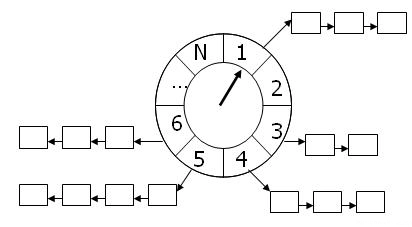
The Time Wheel is an interesting algorithm, first presented in a paper by George Varghese and Tony Lauck. Its core logic involves:

• Using a fixed-size array to represent the time wheel, where each slot corresponds to a time interval.
• Each slot contains a slice to hold tasks expected to expire in that time period, along with a Map<uid, slot> to track which UID corresponds to which slot.
• A timer periodically advances the time wheel one position (interval), processing all tasks in the current slot.

In this case, we can set the interval to 1 second and the time wheel to have 600 slots. When a driver reports data, the record is inserted into the slot corresponding to the current position minus one.
Here’s a simple demo:
https://gist.github.com/hxzhouh/5e2cedc633bae0a7cf27d9f5d47bef01

Advantages

• Adding tasks using the time wheel has a time complexity of O(1).
• The number of slots is fixed, ensuring memory usage remains manageable.
• It’s suitable for handling a large number of scheduled tasks.

Disadvantages

• The size of the interval limits the time wheel’s precision.
• Deleting tasks can degrade to O(n) complexity if tasks are unevenly distributed.

Thus, the time wheel is particularly suited for:

• Rapid insertion of many tasks.
• Scenarios with low precision requirements.
• A reasonably uniform distribution of tasks.

Optimization of the time Wheel

Simple Time Wheel

This maintains a fixed-length array corresponding to all tasks’ maximum expiration values (intervals). For example, if there are 10 tasks with expiration times of 1s, 3s, and 100s, an array of length 100 is created, where each index corresponds to each task’s expiration. As the clock ticks, expired tasks are identified and processed.

• To schedule a task, Convert it to its expiration value and place it in the relevant array index (O(1)).
• When the clock ticks, pull and execute tasks from that index (O(1)).

Hash Ordered Time Wheel

While the simple time wheel is efficient, maintaining an extensive array with very high expiration times can consume a lot of memory. An improved version uses a hash scheme to map tasks into a fixed-size array, maintaining a ‘bucket’ for each index that contains tasks sorted by absolute expiration time.
Yet this approach can still face challenges, especially when task lists grow long, leading to performance issues.

Hierarchical Time Wheel

This approach employs multiple time wheels, each managing different time intervals, and can effectively mitigate issues seen in simple or hash-ordered time wheels.
Refer to Kafka’s Purgatory for a cascading time wheel implementation:

• The first level of the time wheel is predetermined, while overflow levels are created dynamically as needed.
• Tasks initially allocated to higher-level wheels are divided into lower-level wheels as time elapses.

Summary

Here’s a comparison of various algorithms’ performance

References

1. Real-world implementations of time wheels:
   • Netty’s HashedWheelTimer
   • Kafka’s [Purgatory](https://www.confluent.io/blog/apache-kafka-purgatory-hierarchical-timing-wheels/
   • go-zero’s NewTimingWheel
2. Hashed and Hierarchical Timing Wheels

• Long Time Link
• If you find my blog helpful, please subscribe to me via RSS
• Or follow me on X
• If you have a Medium account, follow me there. My articles will be published there as soon as possible.