What’s consistent hashing

First, let me quote a definition from Wikipedia:

In computer science, consistent hashing is a special kind of hashing technique such that when a hash table is resized, only 𝑛/𝑚 keys need to be remapped on average where 𝑛 is the number of keys and 𝑚 is the number of slots. In contrast, in most traditional hash tables, a change in the number of array slots causes nearly all keys to be remapped because the mapping between the keys and the slots is defined by a modular operation.

Consistent hashing evenly distributes cache keys across shards, even if some of the shards crash or become unavailable.

In distributed systems, consistency hash is everywhere. CDN, KV, load balancing, and other places have their shadows. Consistency hash is one of the cornerstone algorithms of distributed systems. It has the following advantages.

• Balanced load: Consistency hash algorithm can evenly distribute data on nodes.
• Scalability: In the consistency hash algorithm, only part of the data needs to be re-mapped when the number of nodes increases or decreases. It is easier for the system to expand horizontally, and the number of nodes can be increased to meet greater load requirements;
• Reduce data migration: Compared with the traditional hash algorithm, the consistent hash algorithm has less data that needs to be re-mapped when nodes increase or decrease, which can greatly reduce the cost of data migration and reduce the instability and delay of the system;

This article aims to learn the consistency hash algorithm and its simple implementation.

This article is first published in the medium MPP plan. If you are a medium user, please follow me in medium. Thank you very much.

Principle of Consistent Hashing Algorithm

Basic Consistent Hashing Algorithm

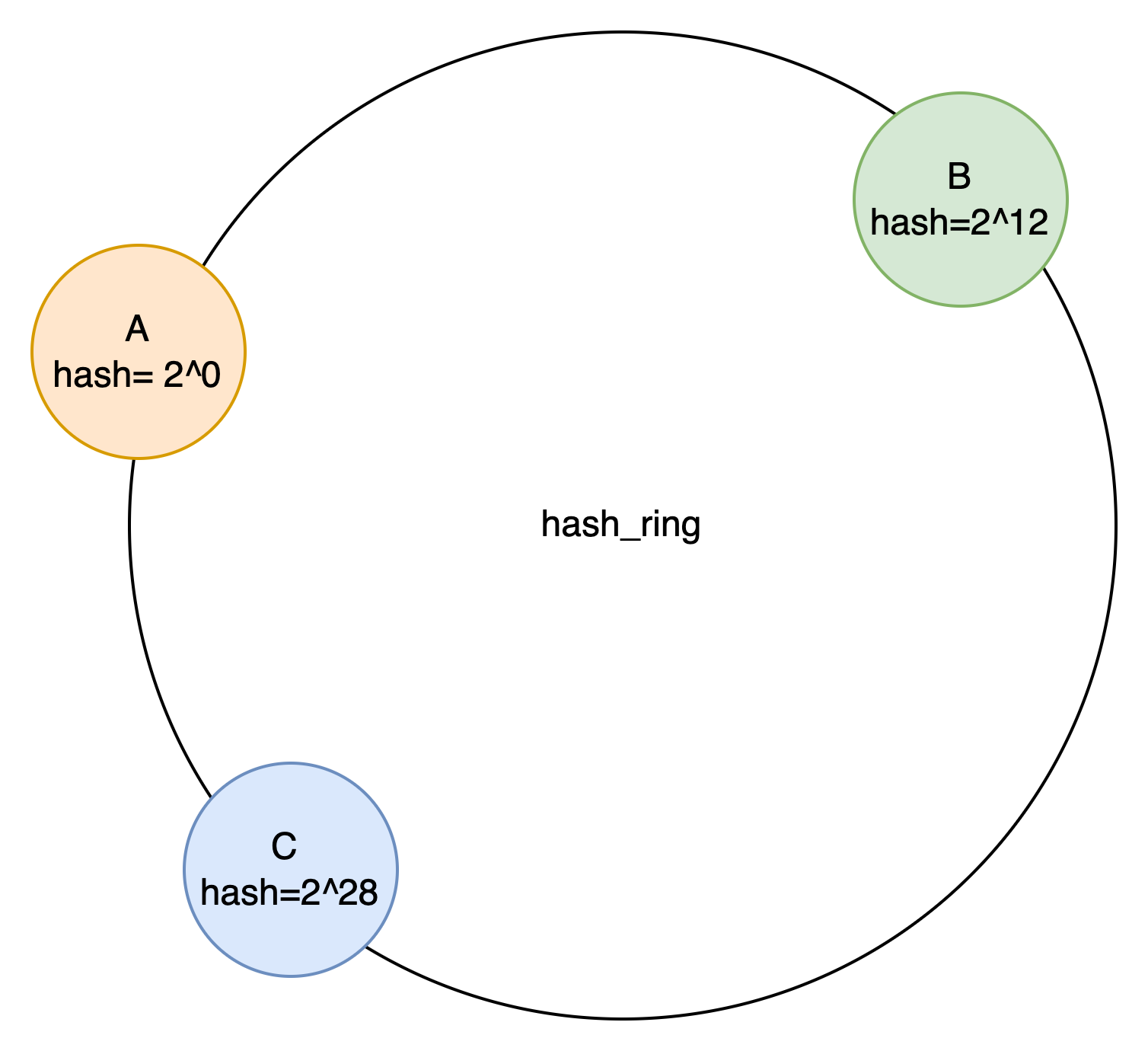
The most basic consistent hashing algorithm is to distribute nodes directly on a ring, thus dividing the value range. After the key goes through hash(x), it falls into different value ranges and is processed by the corresponding node. The most common size of the value range space is: 2^32 - 1. Nodes fall into this space to divide the value ranges belonging to different nodes. As shown in the figure.

Node

The hash range stored by Node A is [0,2^12).

The hash range stored by Node B is [2^12,2^28).

The hash range stored by Node C is [2^28,0).

The basic consistent hashing algorithm mentioned above has obvious drawbacks:

1. The random distribution of nodes makes it difficult to distribute the hash value domain evenly. As can be seen from above, the data stored by the three nodes is uneven.
2. After dynamically adding nodes, it is difficult to continue ensuring uniformity even if the original distribution was uniform.
3. One serious drawback caused by adding or removing nodes is:
   1. When a node becomes abnormal, all its load will be transferred to an adjacent node.
   2. When a new node joins, it can only share the load with one adjacent node.

Virtual Nodes

Rob Pike said: “In computer science, there are no problems that cannot be solved with another layer of indirection.” Consistent hashing follows this principle as well.

If the three nodes are imbalanced, we can virtualize them into N virtual nodes: A[a1,a2….a1024]. Then, we map them onto a hash ring in this way.

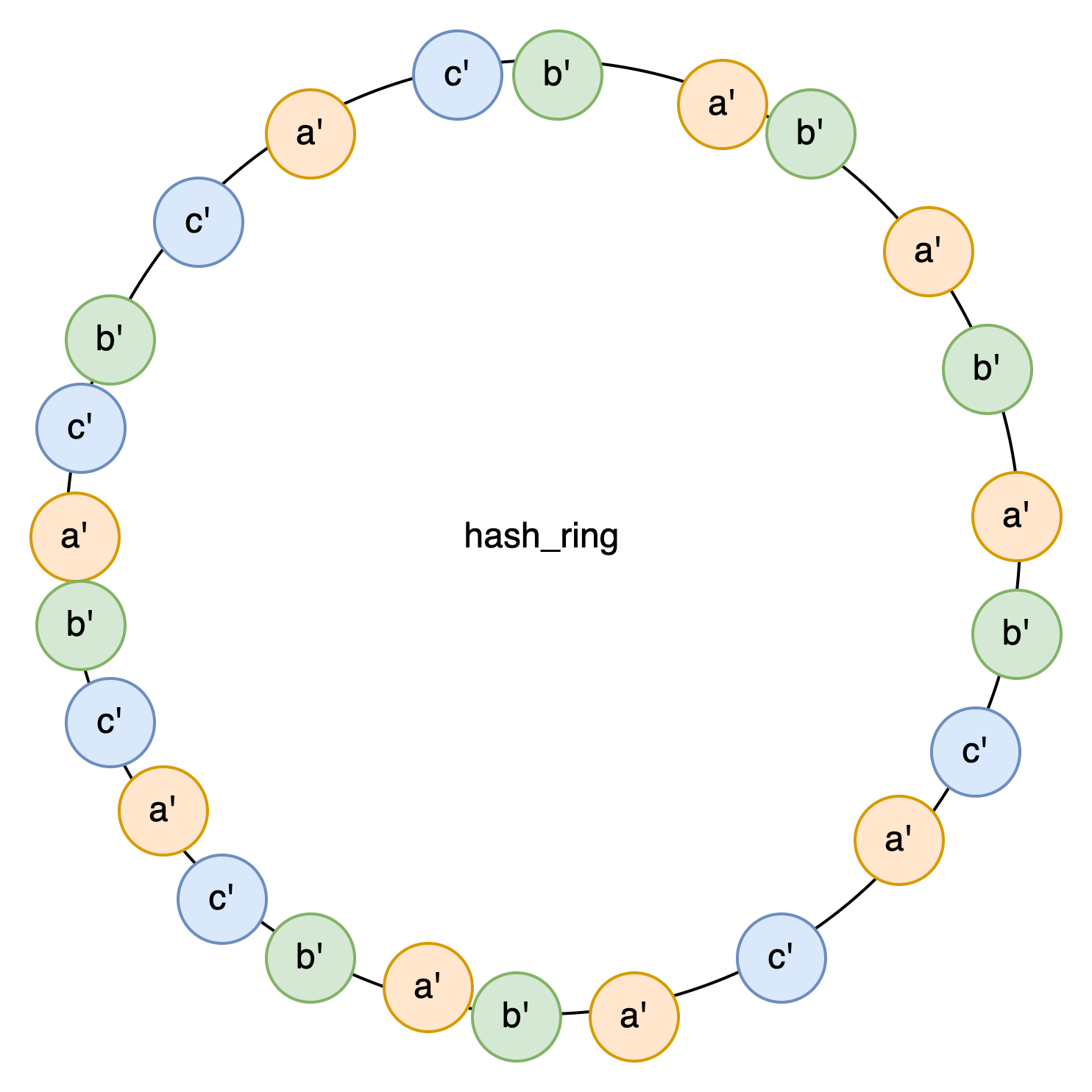
Each virtual node has a corresponding hash range. It is responsible for a segment of keys and then reads and writes data based on the virtual node’s name to find the corresponding physical node.

The above three problems are perfectly solved with the introduction of virtual nodes.

1. As long as we have enough virtual nodes, the data of each node can be balanced (⚠️: this comes at a cost in engineering).
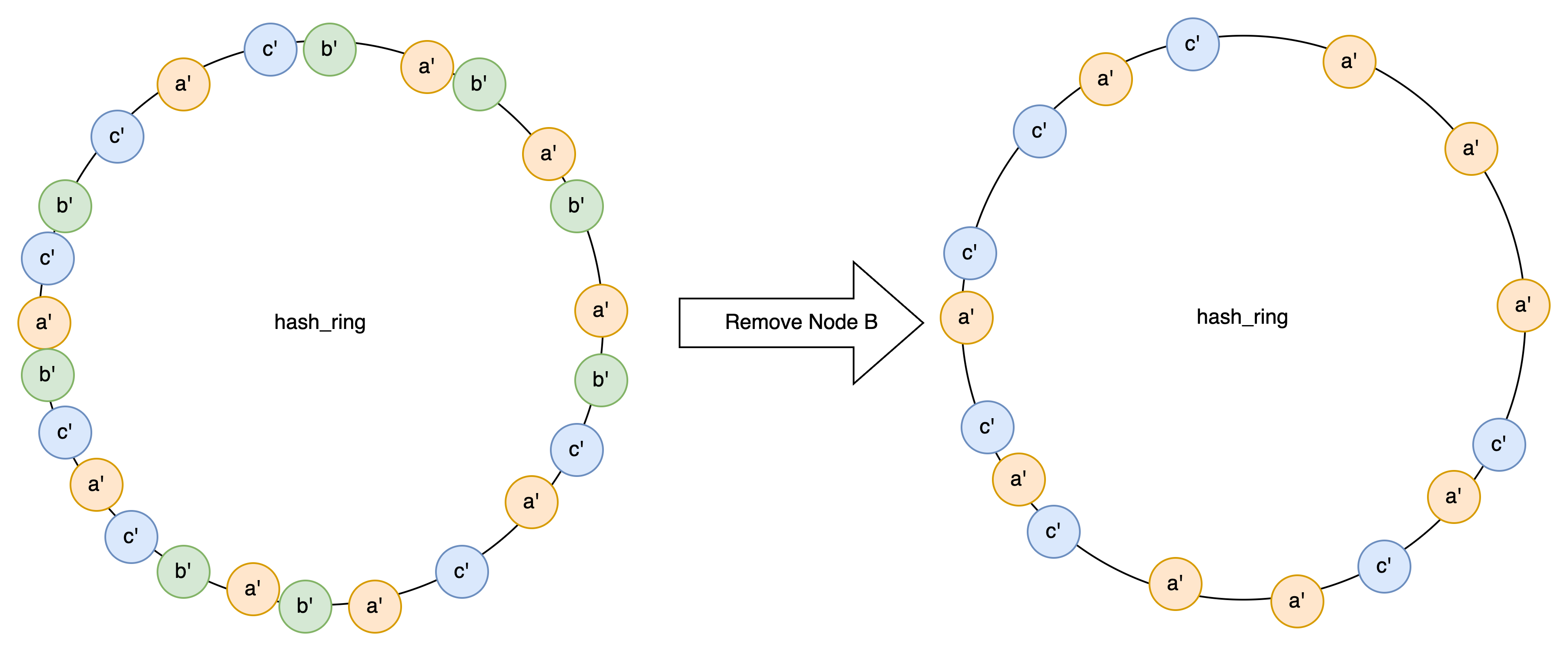
2. If a node goes down, its data will be evenly distributed among all nodes in the cluster. Similarly, newly added nodes can also handle the load of all nodes.
   
   Go language implementation

Complete code

First, define a hash_ring and use crc32.ChecksumIEEE as the default hash function.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

type VirtualNode struct { 
    Hash uint32  
    Node *Node  
}
type Node struct {   // Physics Node
    ID   string  
    Addr string  
}
type HashRing struct {
	Nodes        map[string]*Node
	VirtualNodes []VirtualNode. 
	mu           sync.Mutex
	hash         HashFunc
}
func NewHashRing(hash HashFunc) *HashRing {  
    if hash == nil {  
       hash = crc32.ChecksumIEEE  
    }  
    return &HashRing{  
       Nodes:        make(map[string]*Node),  
       VirtualNodes: make([]VirtualNode, 0),  
       hash:         hash,  
    }  
}

Let’s take a look at how to add a physics node:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14

func (hr *HashRing) AddNode(node *Node) {  
    hr.mu.Lock()  
    defer hr.mu.Unlock()  
  
    hr.Nodes[node.ID] = node  
    for i := 0; i < VirtualNodesPerNode; i++ {  
       virtualNodeID := fmt.Sprintf("%s-%d", node.ID, i)  
       hash := hr.hash([]byte(virtualNodeID))  
       hr.VirtualNodes = append(hr.VirtualNodes, VirtualNode{Hash: hash, Node: node})  
    }  
    sort.Slice(hr.VirtualNodes, func(i, j int) bool {  
       return hr.VirtualNodes[i].Hash < hr.VirtualNodes[j].Hash  
    })  
}

For each added node, the corresponding number of virtual nodes must be created, and it is necessary to ensure that the virtual nodes are ordered (so that they can be searched).

Similarly, when removing, virtual nodes also need to be deleted.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

func (hr *HashRing) RemoveNode(nodeID string) {  
    hr.mu.Lock()  
    defer hr.mu.Unlock()  
  
    delete(hr.Nodes, nodeID)  
    virtualNodes := make([]VirtualNode, 0)  
    for _, vn := range hr.VirtualNodes {  
       if vn.Node.ID != nodeID {  
          virtualNodes = append(virtualNodes, vn)  
       }  
    }  
    hr.VirtualNodes = virtualNodes  
}

When querying, we first locate the corresponding virtual node, and then find the corresponding physical node based on the virtual node.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18

func (hr *HashRing) GetNode(key string) *Node {  
    hr.mu.Lock()  
    defer hr.mu.Unlock()  
  
    if len(hr.VirtualNodes) == 0 {  
       return nil  
    }  
  
    hash := hr.hash([]byte(key))  
    idx := sort.Search(len(hr.VirtualNodes), func(i int) bool {  
       return hr.VirtualNodes[i].Hash >= hash  
    })  
    if idx == len(hr.VirtualNodes) {  
       idx = 0  
    }  
  
    return hr.VirtualNodes[idx].Node  
}

Finally, let’s take a look at how the business uses this hash_ring

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56

type KVSystem struct {  
    hashRing *HashRing  
    kvStores map[string]*kvstorage.KVStore  
}  
  
func NewKVSystem(nodes int) *KVSystem {  
    hashRing := NewHashRing(crc32.ChecksumIEEE)  
    for i := 0; i < nodes; i++ {  // init node
       node := &Node{  
          ID:   fmt.Sprintf("Node%d", i),  
          Addr: fmt.Sprintf("192.168.1.%d", i+1),  
       }  
       hashRing.AddNode(node)  
    }  
    kvStores := make(map[string]*kvstorage.KVStore)   //init storage
    for id := range hashRing.Nodes {  
       kvStores[id] = kvstorage.NewKVStore()  
    }  
    return &KVSystem{  
       hashRing: hashRing,  
       kvStores: kvStores,  
    }  
}  
  
func (kv *KVSystem) Get(key string) (string, bool) {   //get value
    node := kv.hashRing.GetNode(key)  
    return kv.kvStores[node.ID].Get(key)  
}  
  
func (kv *KVSystem) Set(key string, value string) {  // set value 
    node := kv.hashRing.GetNode(key)  
    kv.kvStores[node.ID].Set(key, value)  
}  
  
func (kv *KVSystem) Delete(key string) {  
    node := kv.hashRing.GetNode(key)  
    kv.kvStores[node.ID].Delete(key)  
}  
// DeleteNode requires reallocating the data stored on the node.
func (kv *KVSystem) DeleteNode(nodeID string) {   
    allData := kv.kvStores[nodeID].GetAll()  
    kv.hashRing.RemoveNode(nodeID)  
    delete(kv.kvStores, nodeID)  
    for key, value := range allData {  
       kv.Set(key, value)  
    }  
}  

func (kv *KVSystem) AddNode() {  
    node := &Node{  
       ID:   fmt.Sprintf("Node%d", len(kv.hashRing.Nodes)),  
       Addr: fmt.Sprintf("192.168.1.%d", len(kv.hashRing.Nodes)+1),  
    }  
    kv.hashRing.AddNode(node)  
    kv.kvStores[node.ID] = kvstorage.NewKVStore()  
}

In this way, we have achieved the simplest key-value storage based on consistent hashing. Isn’t it very simple? But it supports the operation of our entire network world.